1) Sin 2x cos 2x = 1 2) Tan2x = 1 sec 2x 3) Cot2x = 1 cosec 2x Along with the knowledge that the two acute angles are complimentary ie they add to 90° and you can solve any right triangle If you know two of the three sides, you can find the third side and both the acute anglesIntegral of tan^2x, solution playlist page http//wwwblackpenredpencom/math/Calculushtmltrig integrals, trigonometric integrals, integral of sin(x), integFormula of tan2x 2tanx/1tan^2x 31K views View upvotes 9 4 Newton Kumar Answered 2 years ago 59K views View upvotes 9 4 Subhasish Debroy, Former SDE at Bharat Sanchar Nigam Limited Answered 1 year ago Author has 37K answers and 24M answer views tan2x = 2tanx/(1tan^2x) How!

Online Tutoring Math English Science Tutoring Sat Psat Gmat Toefl Ielts Tutors Homework Help
What is 1-tan^2x
What is 1-tan^2x-Legend x and y are independent variables, ;Trigonometric Identities Solver \square!
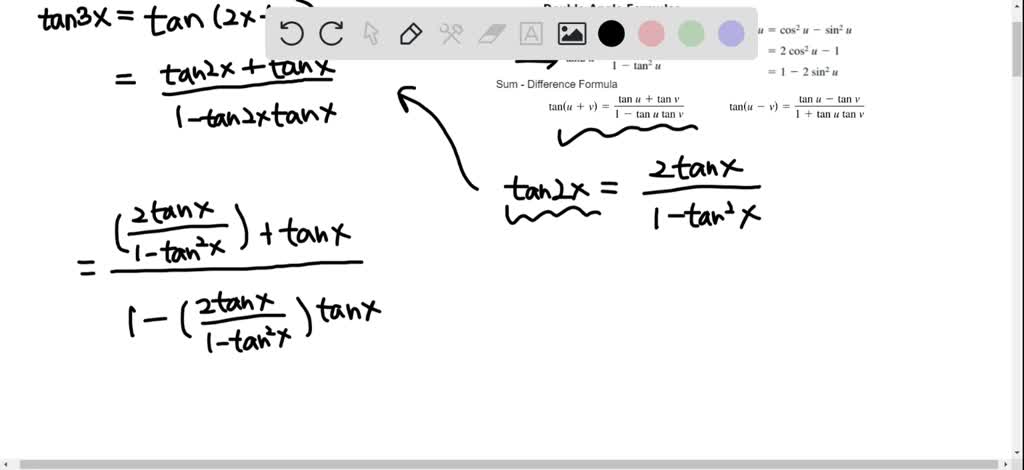



Solved Rewrite Tan 3x In Terms Of Tan X
The sides of this rhombus have length 1 The angle between the horizontal line and the shown diagonal is (a b)/2 This is a geometric way to prove the particular tangent halfangle formula that says tan ( a b 2 ) = sin a sin b cos a cos b {\textstyle \tan \left ( {\dfrac {ab} {2}}\right)= {\dfrac {\sin a\sin b To get the formula for tan 2A, you can either start with equation 50 and put B = A to get tan(A A), or use equation 59 for sin 2A / cos 2A and divide top and bottom by cos² A Either way, you get (60) tan 2A = 2 tan A / (1 − tan² A) Sine or Cosine of a Half AngleGet an answer for 'Prove that tan^2x/(1tan^2x) = sin^2x' and find homework help for other Math questions at eNotes
For the question, tan(2x)tanx = 1, I divided it by tanx, and got the solution as (2n 1) π 6 tan2x = cotx = tan(π 2 − x) So, 2x = nπ π 2 − x So, 3x = (2n 1) π 2Tan 2x=(tan xtan x·1)/(1tan x·tan x) =2·tan x/(1tan 2 x) If we continue, with n=3, H=2·tan x, K=1−tan 2 x, using the formula we have tan 3x=(2·tan xtan x·(1−tan 2 x))/(1−tan 2 x−(2·tan x)tan x) =(3·tan x−tan 3 x)/(1−3·tan 2 x) This formula uses the previous term only (as apposed to the previous two terms for the sine Basic Formula ∫x n = x n1 /n1 C ∫cos x = sin x C ∫sin x = cos x C ∫sec 2 x = tan x C ∫cosec 2 x = cot x C ∫sec x tan x = sec x C ∫cosec
Detailed explanation with examples on propertiesofinversetrigonometricfunctions helps you to understand easily , designed as per NCERT QnA , Notes & VideosSolve for x tan (2x)=1 tan (2x) = 1 tan (2 x) = 1 Take the inverse tangent of both sides of the equation to extract x x from inside the tangent 2x = arctan(1) 2 x = arctan (1)Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!



Trig Identities Hsn Forum




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic
Hence, evaluating the derivative of the function using the quotient rule yields `f'(x) = ( 2tan x/(cos^2 x))/((1 tan x)^2)` Approved by eNotes Editorial Team We'll help your grades soarFree online tangent calculator tan(x) calculator This website uses cookies to improve your experience, analyze traffic and display adsAnyone help plz Click to expand Integral of u^2 is NOT (u^3)/3 c Rather, integral of (u^2)du = (u^3)/3 c In (tan^2)x your 1st mistake is not writing dx Note that dx is NOT always du!!!!!



Solved Simplify The Expression Tan 4x Tan 2x 1 Tan 4xtan 2x A Tan 3 B Tan 6x C Tan 2x D Tan 9 Course Hero




Solve The Trigonometric Equation Tan X Tan 2x Tan X Tan 2x 1
Plot of the six trigonometric functions, the unit circle, and a line for the angle = radians The points labelled 1, Sec(θ), Csc(θ) represent the length of the line segment from the origin to that point Sin(θ), Tan(θ), and 1 are the heights to the line starting from the axis, while Cos(θ), 1, and Cot(θ) are lengths along the axis starting from the origin 1tan^2(x) = 1 (sin2x)/(cos2x) = cos2x sin2x/cos2x = cos 2x/cos2x is a posibly 'simplified' version in that it has been boiled down to only cosinesTan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x) tan(2x) = 2 tan(x) / (1




1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube




What Is The Integration Of Tan 2x Solution Quora
Formula to Calculate tan2x Tan2x Formula is also known as the double angle function of tangent Let's look into the double angle function of tangent ie, tan2x Formula is as shown below tan 2xIn trigonometry formulas, we will learn all the basic formulas based on trigonometry ratios (sin,cos, tan) and identities as per Class 10, 11 and 12 syllabi Also, find the downloadable PDF of trigonometric formulas at BYJU'STan 2x = 2 tan x/1 tan2 x = 2 cot x/ cot2 x 1 = 2/cot x – tan x tangent doubleangle identity can be accomplished by applying the same methods, instead use the sum identity for tangent, first • Note sin 2x ≠ 2 sin x;



Prove Sin2x 2tanx 1 Tan 2x Socratic




Quiz Worksheet Double Angle Formula Study Com
Our given expression is tan(2x y) tan(2x – y) = 1 Formula used When A B = 90° then, tanA tanB = 1 and vice versa Calculation Our given expression is tan(2x y) tan(2x – y) = 1 ⇒ 2x y 2x – y = 90° ⇒ 4x = 90° ⇒ 2x = 45° Now, tan2x = tan45° = 1 ∴ The value of tan45° is 1 Download Question With Solution PDF ››Since x x is on the right side of the equation, switch the sides so it is on the left side of the equation 2tan(x) 1− tan2(x) = tan(2x) 2 tan (x) 1 tan 2 (x) = tan (2 x)Cosine 2x or Cos 2x formula is also one such trigonometric formula, which is also known as double angle formula It is called a double angle formula because it has a double angle in it This is the reason why it is driven by the expressions for trigonometric functions of the sum and difference of two numbers (angles) and related expressions




Using Standard Trigonometric Identities Show That Chegg Com




Online Tutoring Math English Science Tutoring Sat Psat Gmat Toefl Ielts Tutors Homework Help
even though the answer is tanx integration of 1 tan^2x can be written x tan^3/3 isn't it?If you let u=tanx in integral (tan^2)x you getTan adjacent q= adjacent cot opposite q= Unit circle definition For this definition q is any angle sin 1 y q==y 1 csc y q= cos 1 x q==x 1 sec x q= tan y x q= cot x y q= Facts and Properties Domain The domain is all the values of q that can be plugged into the function sinq, q can be any angle cosq, q can be any angle tanq, 1,0,1,2, 2 qpnn




Integration Calculus Notes




Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Trigonometric Equation Calculator \square!D is the differential operator, int is the integration operator, C is the constant of integration Identities tan x = sin x/cos x equation 1 cot x = cos x/sin x equation 2 sec x = 1/cos x equation 3 csc x = 1/sin x equation 4




3 Simplifying Trig Expression 1 Tan 2x Youtube



Tangent Identities
So I'll have to use a formula From what I know about the graph of the tangent , I know that the tangent will equal 1 at 45° after every 180° These solutions for tan( x /2) are at 0° 45°, 180° 45°, 360° 45° , and so forth You can check some important questions on trigonometry and trigonometry all formula from below 1 Find cos X and tan X if sin X = 2/3 2 In a given triangle LMN, with a right angle at M, LN MN = 30 cm and LM = 8 cm Calculate the values of sin L, cos L, and tan L 3 Ex 33, 23 Prove that tan4𝑥 = (4 tan〖𝑥 (1−tan2𝑥)〗)/(1 − 6 tan2 𝑥tan4 𝑥) Taking LHS tan 4x We know that tan 2x = (2 𝑡𝑎𝑛𝑥)/(1 − 𝑡𝑎𝑛2 𝑥) Replacing x with 2x tan (2 × 2x) = (2 𝑡𝑎𝑛2𝑥)/(1 − 𝑡𝑎𝑛2 2𝑥) tan 4x = (2 𝑡𝑎𝑛2𝑥)/(1 − 𝑡𝑎𝑛2 2𝑥) = (2 ta




Sum And Difference Identities Video Lessons Examples And Solutions




Trigonometric Functions With Their Formulas
As far as I know, so far the $\tan2x$ can be converted to $\frac{2\tan x}{1\tan^2x}$ using the double angle formula and the $\tan 2x$ can be further be substituted to the following given item ($\tan(xa·)\tan(xb)$) however the problem now is that there are no ways to simplify this to my knowledgeList of Trigonometric sin2x cos2x tan2x tan3x theta formula/identity Proof in terms of tanx, sin3x cos3x formula/identity, sin2xcos2x sin square x plus cos square x, cos sin a cos sin b sin cos a plus minus sin cos bIntegration of tan inverse (2x / (1 x^2)) dxintegration of tan inverse (2x / (1 x^2)) dx this video teaches you how to perform the integration of tan in




Cos2x Sin2x 1 1 Tan2x Sec2x Cot2x 1 Csc2x Cofunction




Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi
Explanation Change to sines and cosines then simplify 1 tan2x = 1 sin2x cos2x = cos2x sin2x cos2x but cos2x sin2x = 1 we have ∴ 1 tan2x = 1 cos2x = sec2x Answer linkTan 2x ≠ 2 tan x By putting formula We can also calculate TANGENT by using the formula or entering the formula of TAN in the required cell Below is the formula =TAN(number) Step 1 Firstly, we should have Radians ready for the required angle, which we have seen above, that how to calculate in step 3 to 5, which has a formula of = RADIANS(angle)



Solve The Following For X Cos 1 X 2 1 X 2 1 Tan 1 2x X 2 1 2p 3 Sarthaks Econnect Largest Online Education Community




Integrate Int Tan 1 2x 1 X 2 Dx
$\tan^2{x} \,=\, \sec^2{x}1$ $\tan^2{A} \,=\, \sec^2{A}1$ In this way, you can write the square of tangent function formula in terms of any angle in mathematics Proof Take, the theta is an angle of a right triangle, then the tangent and secant are written as $\tan{\theta}$ and $\sec Introduction to Tan double angle formula let's look at trigonometric formulae also called as the double angle formulae having double angles Derive Double Angle Formulae for Tan 2 Theta \(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formulaCos 2x ≠ 2 cos x;




Prove The Identity 4 Tan 3x 12 Tan X 4 Tan 3 Chegg Com




Integration Calculus Notes
Cosine 2X or Cos 2X is also, one such trigonometrical formula, also known as double angle formula, as it has a double angle in it Because of this, it is being driven by the expressions for trigonometric functions of the sum and difference of two numbers (angles) and related expressions Let us start with the cos two thetas or cos 2X or cosineDouble angle formulas We can prove the double angle identities using the sum formulas for sine and cosine From these formulas, we also have the following identities sin 2 x = 1 2 ( 1 − cos 2 x) cos 2 x = 1 2 ( 1 cos 2 x) sin x cos x = 1 2 ( sin 2 x) tan 2 x = 1 − cos 2 x 1 cos 2 x Double Angle Formulas The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself Tips for remembering the following formulas We can substitute the values ( 2 x) (2x) (2x) into the sum formulas for sin \sin sin and



Solved Givencos 3 0 5 Findtan2 6 Use The Formulatan2x 1 Cos2x 1 Cos2x Course Hero



How To Prove That Lhs Rhs Sin2x 2tanx 1 Tan Square X Quora
tan 2 x 1 = sec 2 x Of course, if you like memorization better than derivation then memorize all three identities, but you still should understand how to derive them Using this identity with your problem, we get (2tan x) / (1tan 2 x) = 2tan x / sec 2 x = 2(sin x / cos x) / (1/cos 2 x) = 2(sin x / cos x)(cos 2 x) = 2 sin x cos x




Find Sin 2x Cos 2x And Tan 2x If If Tan X 2 And Gauthmath




Art Of Problem Solving



Biomath Trigonometric Functions



Tan2x ただの悪魔の画像




Sec 1 1 Tan 2x 1 Tan 2 X



What Is The Formula Of Tan2x Quora




Example 13 Solve Tan 1 2x Tan 1 3x Pi 4 Class 12



1
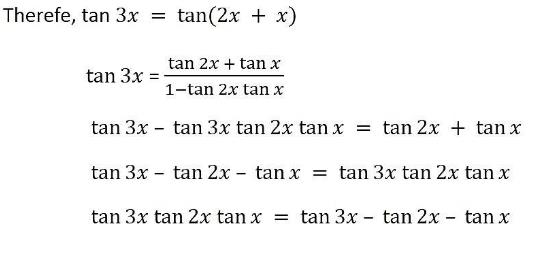



Prove That The Differentiation Of Tan3x Tan2x Tanx Is 3sec 3x 2sec 2x Sec X Edurev Class 12 Question
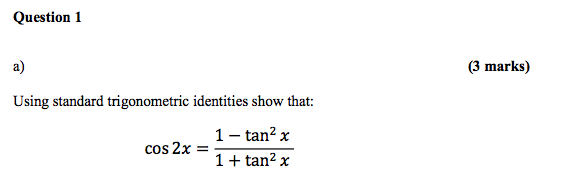



A Using Standard Trigonometric Identities Show That Chegg Com




Chapter 7 Trigonometric Identities And Equations Ppt Download




The General Solution Of The Equation Tan 2 X 1 Is




Online Tutoring Math English Science Tutoring Sat Psat Gmat Toefl Ielts Tutors Homework Help



Simplify The Trigonometric Expression Tan 2x Tan X Using Double Angle Identities A Brainly Com




Math34 Trigonometric Formulas
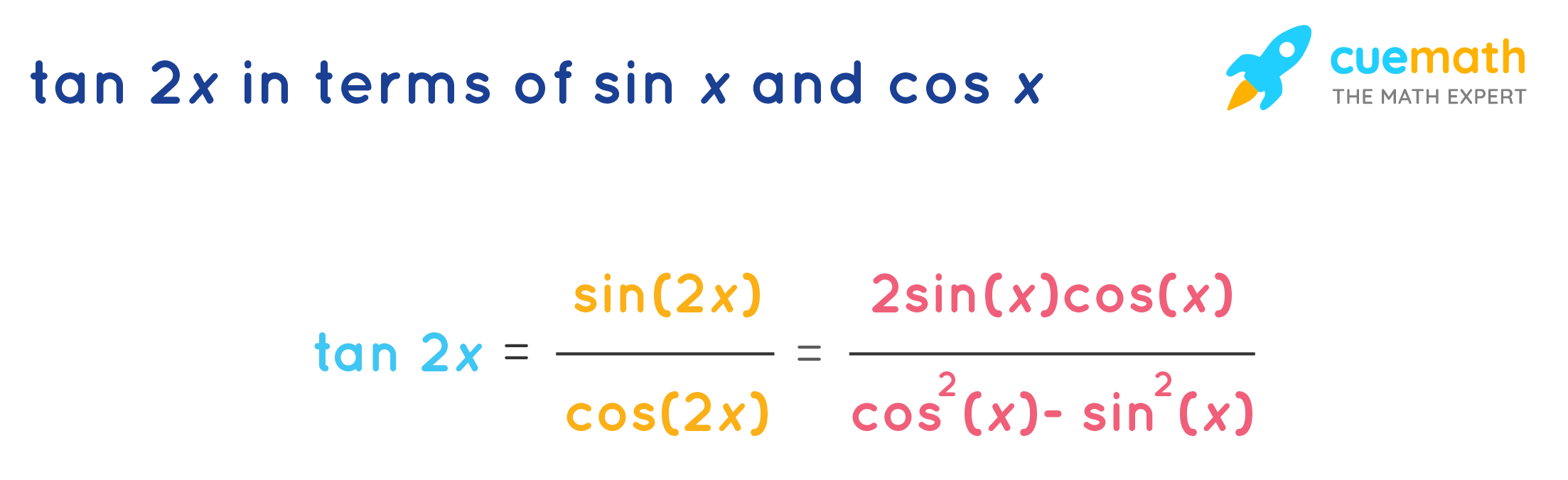



Tan 2x Formula What Is Tan 2x Formula Examples



If X Y 45 Then How Would One Prove That 1 Tanx 1 Tany 2 Quora




Double Angle Identities Worksheet Promotiontablecovers




Sec 2 2x 1 Tan2x Youtube




Tangent Half Angle Formula Wikipedia




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Weierstrass Substitution Wikipedia




Write Cos2x In Tan And Prove Trigonometric Identity For Double Angle Youtube




Trigonometric Integrals Geogebra




Prove Tan2x 2tanx 1 Tan 2 X Maths Introduction To Trigonometry Meritnation Com




Double Angle Formulas What Are Double Angle Formulas Examples



Www Alamo Edu Contentassets 35e1aad11a064ee2ae161ba2ae3b2559 Analytic Math2412 Double Angle Power Reducing Half Angle Identities Pdf




Prove The Identity 3 Tan 3x 9 Tan X 3 Tanx 13 Chegg Com
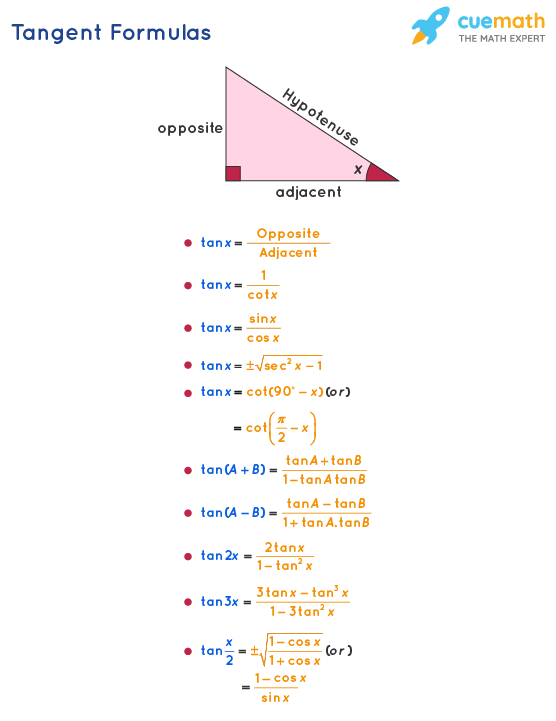



Tangent Formula What Are Tangent Formulas Examples



Solution Prove The Identity 5tan 3x 15tan X 5tan 3 X 1 3tan 2 X




Qprove That Tan X 2 Tan 2x 4 Tan 4x 8 Cot 8x Cot X Mathematics Topperlearning Com Blpusg55
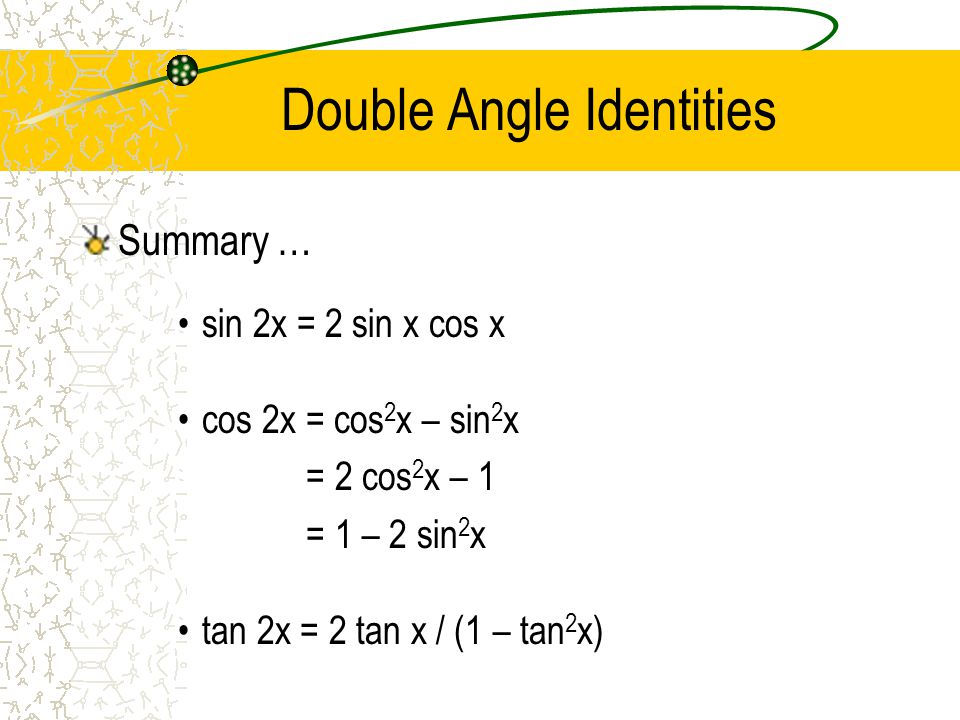



Section 2 Identities Cofunction Double Angle Half Angle Ppt Video Online Download




Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x




Misc 44 Mcq Value Fo Tan 1 2x 1 1 X X2 Dx Is



1




Tan 2x Formula What Is Tan 2x Formula Examples




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
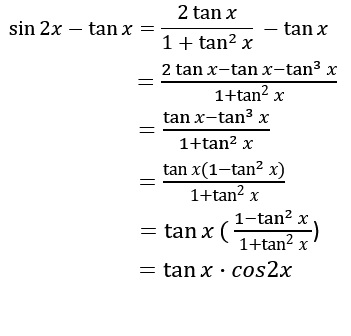



Sin2x Tanx Complete The Identity Socratic




Solution Solve For X In The Given Equation Arc Tan 2x Arctan X P




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Find The General Solution For Each Of The Following Equations Sec2 2x 1 Tan 2x Mathematics Shaalaa Com



3




Math34 Trigonometric Formulas




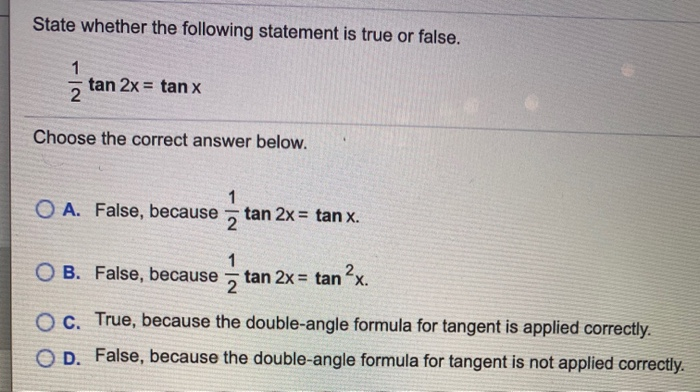



State Whether The Following Statement Is True Or Chegg Com
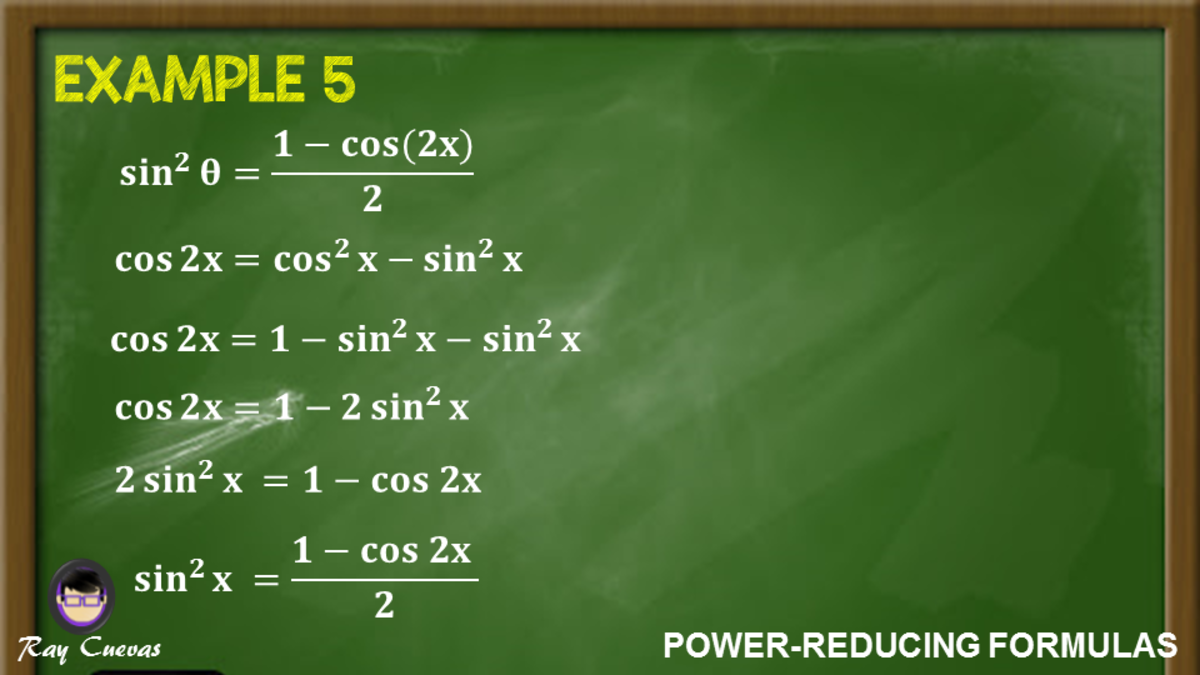



Power Reducing Formulas And How To Use Them With Examples Owlcation




Trigonometric Identities Trigonometric Functions Trigonometry




Find Length Of The Arc Of Y 2 X Mathematics Stack Exchange



What Is Math Int Tan 2 2x Dx Math Quora
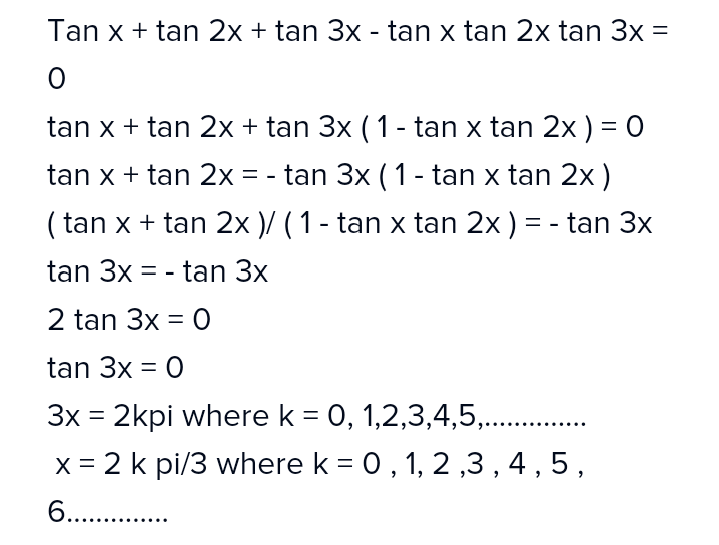



Solve Tanx Tan2x Tan3x Tanxtan2xtan3x




Verify The Following Equation Show Work On The Pa Gauthmath




Double Angles Ppt Video Online Download
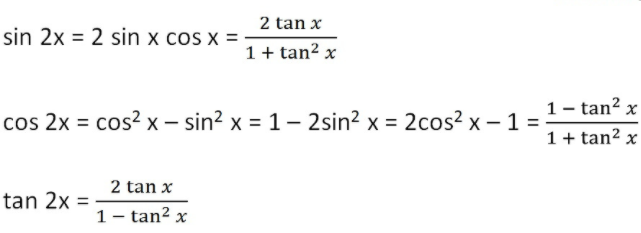



Formula Of Trigonometry Sin Cos Tan Cot Sec Cosec




Sin2x Cos2x 1 Proof




How Many Can You Derive From First Principles Ppt Download




Differentiate The Following From First Principle Tan 2x




Solved Rewrite Tan 3x In Terms Of Tan X



Differentiate The Following W R T X Tan 1 3 2x 1 6x Maths Pyranic




How To Solve Tan 1 2x 1 X2 Cot 1 1 X2 2x Pie 3 Brainly In




Double Angle Formula And Half Angle Formula Video Lessons Examples And Solutions




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube




Verify The Identity 4 2 Tan X Secx2tan X 1 Which Chegg Com



What Is The General Solution Of X For Tan X Tan2x 1 Quora




Cos 2x Formula Trigonometry Formula




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic



Derivatives Of Trigonometric Functions



Q Tbn And9gcr2jamezvnschsup9wyxdzj0wc0knie4dqfphj6okqiboct8vn1 Usqp Cau




Rd Sharma Solutions For Class 11 Maths Updated 21 22 Chapter 11 Trigonometric Equations Download Free Pdf




Tangent Half Angle Formula Wikipedia
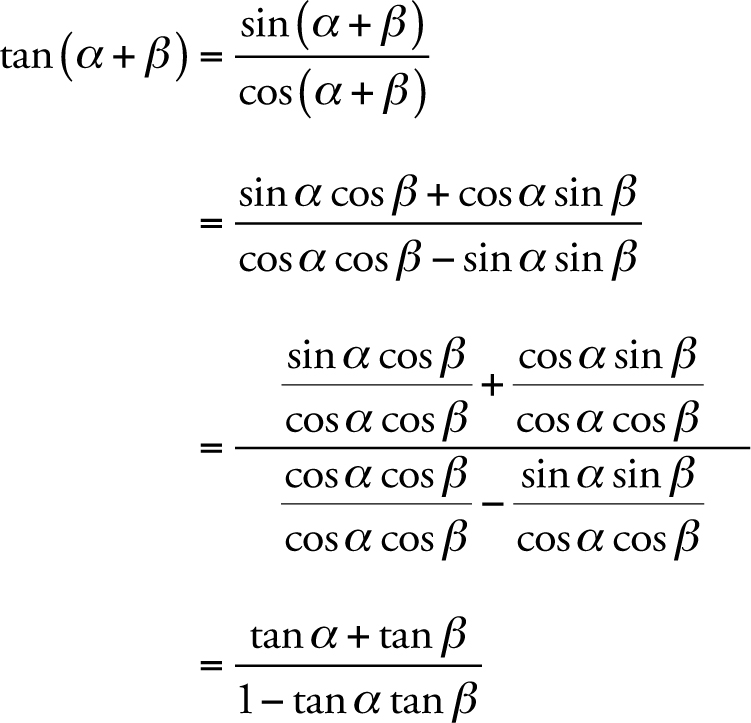



Tangent Identities




A Solution Of The Equation 1 Tan X 1 Tan X Sec 2x 2 Tan 2 0 Where X Lies In The Interval Pi2 Pi2 Is Given By




Multiple Angle Formulas Overview Video Trigonometry Ck 12 Foundation



bestpictjcry Tan 2x Tan 2x



Trigonometric Identities Learn Trigonometry By Ib Elite Tutor
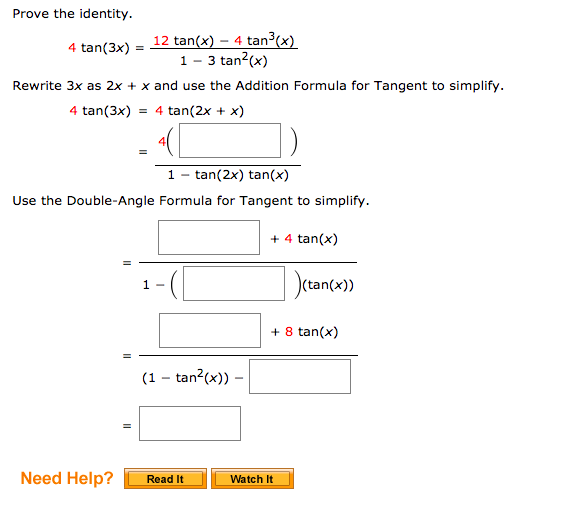



Prove The Identity 12 Tan X 4 Tan X 1 3 Tan2 X Chegg Com
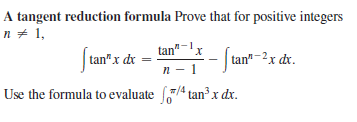



Answered A Tangent Reduction Formula Prove That Bartleby
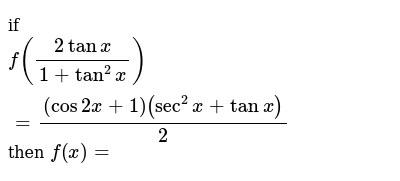



If F 2tanx 1 Tan 2x Cos2x 1 Sec 2x Tanx 2 Then F X




Trig Identity Sec2x Minus Tan2x T10 Youtube




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube




Integrate Tan 2x



0 件のコメント:
コメントを投稿